Site hosted by Angelfire.com: Build your free website today!

Convolution

Introduction

Notes

Content

Convolution - Definition

Let us define the function to equal the convolution between two functions and expressed as

I will sometimes use subscripts to represent variables where this is convenient and clear. This convolution is defined as the integral

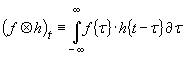
where t represents a “dummy variable” for integration. It might be thought that this convolution could also be expressed in discrete variable as

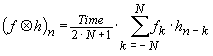
However beware! Most computational software dislikes negative indices and requires that each vector index starts at n = 0. To accommodate this offset we need to add a small modification e.g.

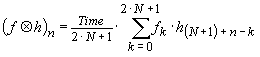
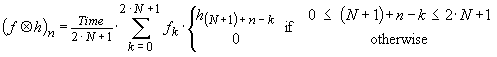
There are still 2·N+1 discrete values for the summation and the offset (N+1) is a small detail to reference the “0” position in the vector. Now f_n, h_n and g_n have indices ranging from n=0 to n=2·N+1 whereas the previous range of index was -N < n < N. However we still need to prevent the index of h exceeding its boundaries so the actual discrete domain formula becomes

Alternatively

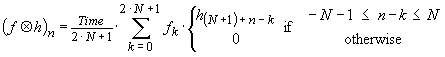
Interestingly the discrete convolution can also be interpreted as a matrix-vector operation i.e.

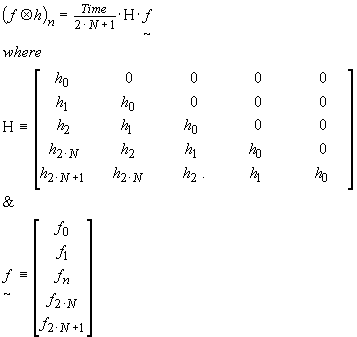
If the matrix H is invertible, then we should be able to predict f from g (where g could be thought of as the output from a system H and f is the input)

Interesting Derivations

Convolution reveals a number of surprising consequences - despite its seemingly simple but obscure proposition; so let's use this proposition to predict a few outcomes.

Introduction

Content

Convolution - Definition

Interesting Derivations

Convolution With A Step Function

Summary