
![]()
If you are like me and sometimes have one of those days with nothing better to do then a good substitute for real work is to start inventing. Now this can either be in a physical location and dealing with physical things or it can be in the workshop of the mind.
The easiest and most pliable of objects to invent with are of course numbers. However what exactly constitutes such an invention - what requirements for validity do we have. For example, in the physical world, someone could claim to have invented a new substance and call it "Obscurocom" and claim some mystical properties. But would such an invention be valid?
First of all,
| Obscurocom must also exist in the physical world and not just be an idle figment of imagination (i.e. available for display, measurement and criticism by others) | |
| Obscurocom must obey (i.e. be consistent with) known physical laws or point to new physical laws resulting from novel behavior (I guess "Blubber" would have suggested such a need) | |
| Obscurocom must present properties that currently available substances do not offer, i.e. it is either disjoint from known substances or known substances are a subset of it |
Obscurocom need not be of any practical use of course (at least for now).
These criteria are necessary to avoid unsupportable claims and time wasting duplication. The same criteria must apply to the invention of new numbers. These must exhibit new properties and remain consistent with standard mathematical properties. For example, they must obey commutative, associative, distributive operations with addition, subtraction, multiplication and division. They must have an inverse. In other words they must obey the properties of a "group". Numbers that do not comply with such operations are probably useless (although things that are not numbers, e.g. matrices, may be allowed to avoid some criteria based on their practical usefulness)
Let us examine some simple analogies. In the beginning we had integers, 1,2,3... etc. These could be added and multiplied etc in groups and also in different ways according to the rules of algebra. The invention of a "negative" allowed -X to be different from the operator "-" acting on "X". In some way the negation formed a new number as opposed to an operation on a number.
Then people thought about "rational numbers". The consisted of a ratio of two integers e.g. ½, ¼, ¾ etc. These were obviously not "integers" but could form integers. For example 3 = 12 / 4. Therefore rational numbers were "new" and integers became a subset of rational numbers.
Hippasus, a student of Pythagoras started to ponder the "square root of two" - was this
number rational? Hippasus thought it was not rational in
his search for a new number. His proof was simple - proof by contradiction. He assumed
the opposite, i.e.
![]() where
P and Q were integers with no common factors (i.e. irreducible). By applying the
rules of algebra he multiplied both sides by Q so the equality would remain (Q
is not zero of course!)
where
P and Q were integers with no common factors (i.e. irreducible). By applying the
rules of algebra he multiplied both sides by Q so the equality would remain (Q
is not zero of course!)
√2 · Q = P
Then he reasoned that if both sides were equal he could square both sides
2 · Q2 = P2
Anything multiplied by 2 is even so P2 must be even.
Since odd numbers have odd squares (e.g. 112 = 121) and even numbers have even squares (e.g. 82 = 64) it followed that P must also be even.
Since P is even we must be able to divide P by 2 and get another integer k = P / 2 i.e. P = 2 · k
Therefore 2 · Q2 = (2 · k)2
So that 2 · Q2 = 4 · k2
And so further that Q2 = 2 · k2
So now, as we reasoned before that P2 was even, we must conclude that Q2 is also even
Since Q2 is an even square, as before, Q must also be even.
Well what have we here now? P turned out to be even and now it seems that Q is also even. So both P and Q must have a common factor of 2.
But recall at the beginning - we explicitly demanded that P and Q had no common factors but here they are caught out with a common factor of 2!
This contradicts the original bargain, so assuming the opposite didn't work. Hippasus concluded that √2 couldn't possibly be rational as P / Q was not "irreducible" i.e. always would have a common factor, in this proof, of 2.
From this contradiction, the initial assumption that √2 could be expressed as a rational number is false; that is to say, √2 is irrational
This
proved that
![]() was a new number but it still obeyed all the rules of algebra.
was a new number but it still obeyed all the rules of algebra.
The term "irrational" was coined to represent such numbers. Pythagoras was infuriated at his student Hippasus - in his mind all numbers should have nicely perfect values. How dare Hippasus deny such a cherished belief? Something had to be done about such nonsense! A perfect solution came to mind and Hippasus was thrown overboard and drowned.
So it seemed, like the layers of an onion, rational numbers became a subset of irrational numbers. For example, any integer can be expressed as the square root of its square (of course) but many square roots cannot be expressed in terms of integers or rational numbers composed of integers.
The search for new numbers continued and along came "pi" π and the "exponential" e, the "golden ratio" φ ≡ ½ · (1 + √5) etc.
As if this was not enough, what was the square root of a negative number? For example what strange numerical creatures lurked inside the solution to x2 < 0? The question had to be asked and the first hooked answer "j " satisfied the simple equation j 2 = -1. From this imaginary goldfish a whole family was born, based on the Cartesian notation z = x + j · y or its equivalent Polar form z = r · e j · Ø .
I hope this historical background provides a useful framework in which to search for new and novel numbers - perhaps unlike fish they are out there to be mined in them there hills of mathland.
Just as a gold miner needs a pick-axe and shovel, a miner for numbers also needs suitable tools. The mainstay operators are typically addition, subtraction, multiplication and addition. Further to this swaggering complement are the rules of algebra.
However are such tools good enough for the job at hand? After all, today's mining relies on heavy machinery. This performs the same basic functions as a pick axe and shovel but on a much greater scale. Further, otherwise untraceable veins of wealth so deeply buried can only be extracted by enhanced mechanical means.
So it may be with the four basic binary operators. This is why I propose to
add an extra two. I call these "Ûp" (i.e.
![]() )
and Ðown" (i.e. ¯)
and are defined
quite simply as
)
and Ðown" (i.e. ¯)
and are defined
quite simply as
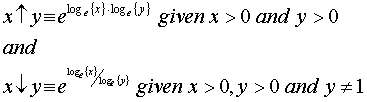
or equally in web page form
x ![]() y ≡ exp{ Loge{ x
} · Loge{ y } }
y ≡ exp{ Loge{ x
} · Loge{ y } }
and
x ¯ y ≡ exp{ Loge{ x } / Loge{ y } }
It is perhaps instructive to remember those old slide rules that used to be used in the 1960's before the calculator. These multiplied two numbers X and Y as follows
X · Y = 10Log{X} + Log{Y}
Similarly the slide rule divided two numbers X and Y using
X / Y = 10Log{X} - Log{Y}
This operation is perfectly valid so long as X and Y are not zero, although they can be negative to allow operations with complex numbers.
The use of "Base 10" is a bit clumsy in mathematics and most people prefer the use of the exponential and natural logarithms. The "binary operators" Ûp and Ðown I propose to use are therefore not exotic and the addition "+" is simply replaced with a multiply "·" and the subtraction "-" with a divide "/". The only mathematical constraint is that y cannot have a value equal to 1 for Ðown as this results in a divide by zero!
For completeness I will also allow unitary operators defined the same way
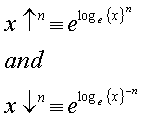
and note that
![]()
and just mention an equivalent "absolute value" unitary operator
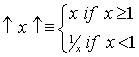
with the result that
![]()
This is exactly analogous to
![]()
These are the extra tools with which we will hunt. However, if you wish to see some more of the properties of Ûp and Ðown before our numerical excavation then why not check out this link Group Properties
Armed with our new tools we begin the great search for potentially new and novel numbers subject for subsequent analysis and conjecture. In another numerical mine in a time long ago an "imaginary" number "j" was unearthed and became unified with ordinary numbers to cerate a complex numerical Gemini z = x + j · y. The numerical prospectors proposed its existence as a solution in the obscure and less than obvious equation
j 2 = -1
It was thought at the time that all known solutions had to be zero or positive. How could such a solution exist with a negative sign?
Not surprisingly, two twin solutions are possible
(+j )2 = -1
and
(-j )2 = -1 since (-1 · j ) · (-1 · j ) = (-1 · -1) · ( j · j ) = (1) · (-1) = -1
The positive solution is selected by convention but both solutions for j 2 = -1 are valid.
By analogy
![]() ³
1 for any real x
and
³
1 for any real x
and
![]() is used to represent the unitary operator "Up
squared". To recap
is used to represent the unitary operator "Up
squared". To recap
![]()
Since [Loge{ x } ]2 ³
0 for all
real x then
![]() ³
exp{ 0 } = 1. By analogy with "j" let's propose an equivalent
solution that we will just call "p" i.e.
³
exp{ 0 } = 1. By analogy with "j" let's propose an equivalent
solution that we will just call "p" i.e.
![]()
There should be no solution for p given our assumptions so far but our question now is, if p exists, what will it look like?
Perhaps p could exist in the well known complex number domain? Let us express a potential solution in polar form, i.e. we propose
p = | p | · e j · Ø
This would infer the following sequence of outcomes
p ![]() = ( | p | · e j · Ø )
= ( | p | · e j · Ø ) ![]()
= exp{ [ Loge { ( | p | · e j · Ø ) ]2 }
= exp{ [ Loge { | p | } + j · Ø ]2 }
We therefore must have this result
exp{ [ Loge { | p | } + j · Ø ]2 } = 1/e
Taking natural Logarithms of each side now
[ Loge { | p | } + j · Ø ]2 = -1
Taking the square root of both sides
Loge { | p | } + j · Ø = ± j
Both real and imaginary components of each side must be equal, therefore
Loge { | p | } = 0
i.e. | p | = 1
so that p = ±1
and Ø = ±1
Well isn't this interesting. The proposed solution p exists and has four valid possible values,
p = ±e ± j
Is "p" a new number? It certainly has valid solutions that are consistent with algebra. However it has four possible and equally valid solutions whereas j has only two valid solutions.
Does this represent a "new property" - have we mined out a new numerical substance?
Let us for now assume that other numbers lack four-fold "valuation". Let us propose an equally odd-ball compound defined as
w = x · p ![]() y
y
where x and y represent ordinary numbers, non zero, real or complex. (This is an equivalent form to z = x + j · y - the same operator precedence of multiplication over addition, "Up" over multiplication etc, is hopefully an obvious convention)
Wow! Perhaps I may have just discovered a new number - I'd better hurry up and give it a name!
If "j" is called an imaginary number then I think I'll call "p" a phantasy number
If "z" is called a complex number I think I'll call "w" a profound number
That phantasy numbers and profound numbers exist is certain as I have not broken any arithmetic rules in their discovery. The Conjectural is whether they are in fact different from existing numbers
That last mathematical mining operation may still have some remaining items of interest still deeply buried. I think I will return. I thought I glimpsed something interesting nearby
exp{ [ Loge { | p | } + j · Ø ]2 } = 1/e
for z ≡ p · e j · Ø
I
had to wonder if the phantasy number p was not alone. What if
"generic" complex numbers z were scattered around and
mixed with
the Up operator ![]() resulting in some other solution Ψ. I
thought it would be interesting to postulate that
resulting in some other solution Ψ. I
thought it would be interesting to postulate that
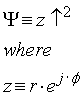
Both r and Ø will be defined as real numbers with the angular tern constrained to 0 ≤ Ø < 2 · π .
I substituted this polar representation for z into the definition for
![]() and obtained
and obtained
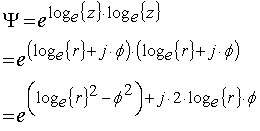
Let's now express Ψ in conventional polar form
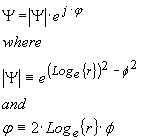
We see that Ψ has a magnitude equal to exp{ [ Log { r } ]2 - Ø2 } and that the term
[ Log { r } ]2 ³ 0
for all real values of r. Now lets look at the range of the angular contribution from Ø. Since we defined 0 ≤ Ø < 2 · π we know that 0 ≤ Ø2 < 4 · π2 .
These two observations tell us that the magnitude of Ψ must be greater than
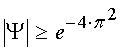
for all complex values of z ≡ r · e j
· Ø where r and Ø are both real and
Ø is constrained to an angular range defined by 0 ≤ Ø < 2 · π
. This leads us into the forbidden
zone of ![]()
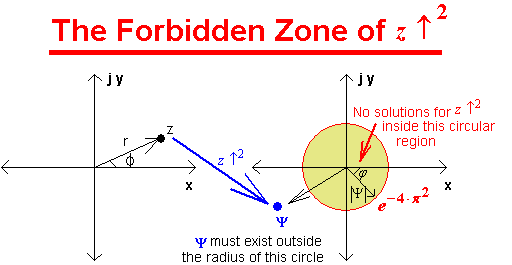
Once again I had to ask, what's inside
this forbidden zone of ![]() ? This is no different
than asking "what numbers are inside the range x 2
< 0 except that we have a 2-dimensional area search as opposed to a single
dimension negative axis search.
? This is no different
than asking "what numbers are inside the range x 2
< 0 except that we have a 2-dimensional area search as opposed to a single
dimension negative axis search.
Let us return to our result for the magnitude of Ψ i.e.
|Ψ| = exp{ [ Log { r } ]2 - Ø2 } where the polar angle of z was restricted to the range 0 ≤ Ø < 2 · π
Surely we should not constrain our search for new numbers to such a restricted angular range? Let us first consider negative angles e.g.
-2 · π ≤ Ø < 0 i.e. 4 · π2 ≥ Ø2 > 0 - the same range for Ø2 as before but just in a "different order"
Clearly no opportunity exists to enter the forbidden zone with negative angular values of Ø.
However, what about the numbers that turn? Why should we assume that angular values with additional integer multiples of 2 · π should be equal? Perhaps they are not, at least in the forbidden zone. For example, what if we let z take a double turn, e.g.
2 · π < Ø ≤ 4 · π
Since the [ Log { r } ]2 ≥ 0 contribution to the magnitude of Ψ remains as before, the squared-angle component Ø2 becomes smaller, i.e.
4 · π2 < Ø2 ≤ 16 · π2
Clearly we have now entered the first layer of the forbidden zone of ![]() and the magnitude of Ψ
is now outside a much smaller second forbidden zone defined by
and the magnitude of Ψ
is now outside a much smaller second forbidden zone defined by
![]()
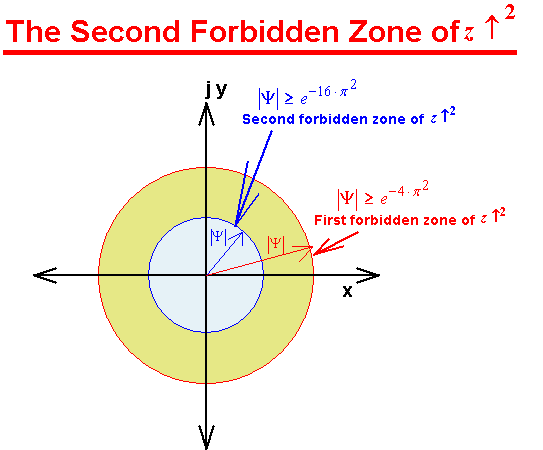
Well isn't this also interesting. Now we have a number that has a multi turn property. Each solution for a forbidden zone is different and any number of forbidden zones clearly now seem definable
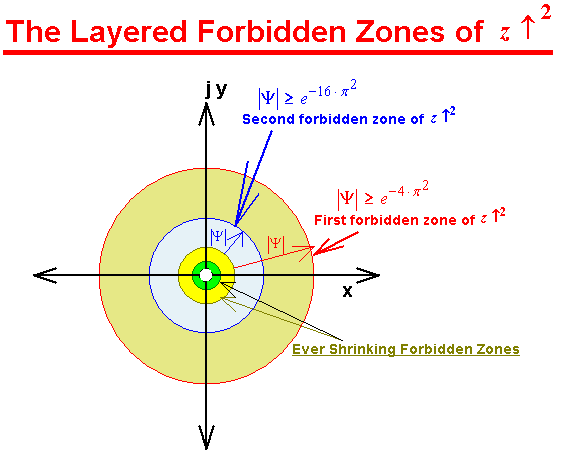
So do these "multi-turn" numbers really exist? Just like the
layers of an onion so are the forbidden zones of ![]()
In this web chapter we have journeyed on a mathematical mining expedition. Did we discover the new deep and buried numbers we searched for?
I introduced two new binary operators Ûp ![]() and Ðown ¯
as well as a unitary Ûp-exponent operator
and Ðown ¯
as well as a unitary Ûp-exponent operator ![]() to help us on our search. These were based on well known exponential and natural
logarithm functions and parallel the use of old slide rule log-antilog approach
to perform multiplication and division tasks. This extends the set of binary
operators to
to help us on our search. These were based on well known exponential and natural
logarithm functions and parallel the use of old slide rule log-antilog approach
to perform multiplication and division tasks. This extends the set of binary
operators to
(+, -, ·, /,
, ¯) and and the set of unitary operators to ( #n, #
).
These could be extended indefinitely I guess e.g.
x
Λ y ≡ exp{ Loge {x} ![]() Loge {y} }
Loge {y} }
and perhaps some subsequent use might be found for this.
In the same way that "j " was proposed to represent one of the solutions to the otherwise absent members of x2 < 0, we proposed a phantasy number "p" as a solution to the otherwise absent members of
![]()
i.e.
![]()
I would have thought "what's good for the goose is good for the gander", so if an imaginary number "j " could exist why shouldn't this phantasy number "p " also exist?
The solution "p " remains consistent with well known
algebraic rules but has four associated solutions whereas
other number solutions have two solutions or less. This may
qualify "p " as a new number, and then perhaps the
composite "profound number" w defined as w
≡ x · p
![]() y. I guess this conjecture is open to debate.
y. I guess this conjecture is open to debate.
Further we looked deeper into the mother load of potential new golden numbers
(hopefully not fool's golden numbers) and proposed solutions to other regions
where none should be found. In this case we looked into a circular forbidden
zone of ![]() for even more numerical treasure. By analogy once more, this is no
different for the proposal that j2 = -1
except that the solution set Ψ
lays inside a forbidden region rather than along a forbidden axis.
for even more numerical treasure. By analogy once more, this is no
different for the proposal that j2 = -1
except that the solution set Ψ
lays inside a forbidden region rather than along a forbidden axis.
Once again we observed odd-ball properties. This solution set Ψ appears to be differentiated inside ever decreasing circular regions i.e. forbidden zones, depending on its winding number. Perhaps Ψ could be called a threaded number?
Do other numbers exhibit such differentiation? Surely Ψ has as much "right to exist" as p just as p has as much "right to exist" as j ?
Well this has been a really fun web chapter to write. I don't make any claims of course as my web chapter on the search for inventing new numbers is yet another entry in my Conjecturals devoted to wonder, fascination and thought ☺
I wonder how much I could get for p or Ψ on Ebay?
I also have to wonder what would happen to me if Pythagoras were to read my web chapter here today?
![]()
Return to: Conjecturals
or: Ian Scotts Technology Pages
© Ian R Scott 2007 - 2008