Radio communication relies on the use of a transmit antenna to send information "over the air" from a local position to another receiving antenna at some remote position. The transmit antenna produces Electromagnetic Energy comprised of an Electrostatic field traveling with a perpendicular Magnetic field at the "speed of light" c ≡ 3 · 108 m s-1 in a vacuum and (very) slightly slower through an atmosphere or other medium with a relative permittivity εr or relative μr permeability greater than one.
An isotropic antenna has a omni-directional antenna that transmits radio signal energy, or receives radio signal energy equally in all directions. Consequently, energy supplied to a loss-less isotropic antenna radiates equally over the surface of a sphere with an surface area related to its radius d according to
Asphere = 4 · π · d 2
The power density Sd at a distance d is determined by the input power Pin supplied to this antenna and the surface area of this sphere
Sd = Pin / [ 4 · π · d 2 ]
Also, the "aperture area" Aaperture (i.e. its ability to capture a portion of radiated energy) for an isotropic antenna is related to wavelength and commonly predicted to be
Aaperture = λ2 / ( 4 · π ) ...(1)
where λ ≡ c/f
Note that c represents the "speed of light" and that c ≈ 3 · 108 m s-1 and f refers to the frequency of the radio wave in Hz (cycles per second)
The portion of radio wave energy "captured" by this aperture area at a distance d is simply equal to the ratio of aperture area to the surface area of the hypothetical sphere with a radius also equal to d. The received power Pr is then
Pr = Pin · c2 / [ 16 · π 2 · d 2 · f 2 ]
i.e. Pr / Pin = c2 / [ 16 · π 2 · d 2 · f 2 ] ...(2a)
We can now propose a "path loss" estimation for the ratio of captured radio wave power compared to the input or transmitted power Pin. Expressed in decibels we have
LossdB = 20 · Log10{ d } - 20 · Log10{ f } - 147.56 dB ...(2b)
(Note: we will express loss as a positive quantity hence the sign reversal)
We will use this "-147.56 dB" factor to compare isotropic antennas with other antenna types. Since loss is presented as a positive quantity, antenna varieties that exhibit "gain" will have a term that is more negative in value while this with additional power loss will have a factor that is less negative.
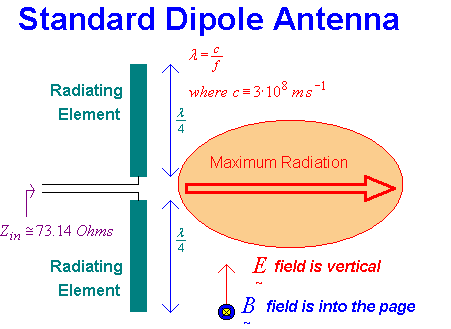
Transmit and receive antennas need not be identical in design but the most common physical arrangement begins with a "dipole" configuration, developed by Heinrich Rudolf Hertz in 1886. This consists of two "quarter wavelength" conductors placed end to end with an electrical connection to the middle section.
If you would like to see derivations for path loss and radiation resistance for isotropic and dipole antennas (electrically short dipoles and half wavelength dipoles), then please click on this hyperlink Electromagnetic Equations
Also, if you would like to see a MathCAD simulation file that predicts radiation resistance for electrically short and half wave dipoles based on these Electromagnetic Equations then please click on this hyperlink Mathcad Radiation Resistance
(These hyperlinks will provide a more detailed description than my following descriptions - and they took me several days to nut out - oh man am I getting slow at maths!)
The wavelength of any electromagnetic wave is governed by the velocity of the wave and inversely proportional to its frequency f. This velocity equals the speed of light so that the associate wavelength λ = c/f . As an example, a dipole antenna intended for operation at f = 150 MHz i.e. λ = 2 meters, would need two conducting elements each equal to ½ meters in length resulting in a requirement of one meter total length. The resulting central feed point impedance becomes (almost purely) resistive given these dimensions and takes a value of Ra ≈ 73.13 Ohms. This feed point resistance is called the "radiation resistance" Ra of the antenna. Electromagnetic energy is converted to or from electric energy through power dissipated in this radiation resistance. For example, a current iac send into this radiation resistance Ra corresponds to an electrical input power Pin equal to
Pin = iac2 · Ra ...(3)
providing that electrical losses in the conducting elements and nearby materials are negligible. Given that receiving and transmitting antenna are "reciprocal" the same conversion between radio wave energy and electrical energy applies.
It may be instructive to illustrate some of the electromagnetic radiation properties associated with the "standard" half wave dipole for subsequent comparison with magnetic loop antenna configurations. Dellinger's formula (1919) expresses a relationship between two radiated magnetic field components and instantaneous time varying AC current Iac flowing along the length x of the dipole antenna (for a half wave dipole we have 0 ≤ x ≤ L = ½ · λ), the AC frequency ω ≡ 2 · π· f at a remote perpendicular distance d and at a given time t.
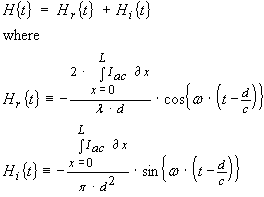...(4)
Note: All units are in standard SI units of meters, Amps, seconds, Hz, and c, the speed of light equals 3 · 108 m s-1
The first magnetic field term Hr { t } is referred to as the "radiation field" and this term is responsible for long range radio wave propagation. The second magnetic field term Hi { t } is referred to as an "induced field" and only becomes significant for short distances. The two terms become equal when d0 = λ / ( 2 · π) . The resulting terminology of "near field" for distances d << d0 is often used, and "far field" for distances were d >> d0.
Radio communication requirements rely exclusively on the "far field" radiation term Hr. We can expect that the induction field term Hi will be negligible due the its d 2 term in the denominator compared to the d term represented in the denominator of the radiation field component.
Let us therefore focus on the radiation term and consider the RMS magnetic field's magnitude which will one half the peak value of the sinusoidal time varying field presented in equation (4), i.e.
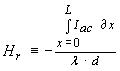...(5)
The AC current Iac in a dipole element has a sinusoidal current distribution starting at x = 0 from one end, rising to a maximum Ip at the dipole's center and falling back to zero at the opposite end where x = λ/2 .
...(6)
Substituting equation (6) into equation (5) and integrating wrt x (along the dipole element's length) produces
...(7)
We may want to equate the AC input power to this dipole antenna to its resulting radiated power density Sd. The series resistive "radiation resistance" or Ra component for a half wave dipole is commonly predicted to approximate Ra = 73.13 Ohms (two significant figure approximation) so the AC input power must equal
Pin = Iac2 · Ra ...(8)
From electromagnetic theory we know that the radiated power density S (power per square meter) is related to the magnetic field strength and the electric field strength by
...(9)
The term Rεμ is called the "impedance of free space" with an approximate value of Rεμ = 377 Ohms. This results in magnetic and electric field equations that are analogous to Ohm's law for voltage, current and resistance
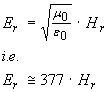...(10)
Converting between magnetic and electrostatic fields can be useful but I will just use the magnetic field "companion" component for now. (This will allow direct comparison with the magnetic loop antenna predictions later on in the main content of this web chapter).
We can now substitute equations (7), (8) into equation (9) to predict the power density Sd produced by a dipole antenna at a perpendicular distance d and with in input AC power Pin .
...(11)
Now lets predict the power that would be captured by an isotropic antenna with an aperture area defined in equation (1) as
Aaperture = λ2 / ( 4 · π ) where λ ≡ c/f
Multiplying the power density in equation (11) by this aperture area now lets us relate captured power to input power applied to the dipole antenna
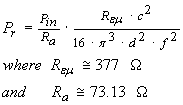...(12)
We can now express this ratio as a loss in dB terms as per equation (2) i.e.
LossdB = 20 · Log10{ d } - 20 · Log10{ f } - 149.71 dB ...(13)
Now recall the previous result for two isotropic antenna from equation (2)
LossdB = 20 · Log10{ d } - 20 · Log10{ f } - 147.56 dB ...(2)
We can see that the path loss for a dipole to isotropic antenna is 2.15 dB lower than the path loss from an isotropic to isotropic antenna combination. We conclude therefore that the dipole antenna has a relative gain of +2.15 dB compared to an isotropic antenna.
This relative gain is not surprising as the dipole has some directivity.
Although the half wave dipole exhibits useful power gain over an isotropic antenna, its dimensions can be cumbersome for portable devices. As we saw previously a VHF dipole designed for operation at a frequency of f = 150 MHz would need a total length of one meter. Small portable devices such a paging receivers would obviously be incompatible with an antenna having such dimensions. In the never ending search for miniaturized electronic devices, an equally compact antenna is essential. How can this be achieved?
The simple dipole can be reduced in length so that it is no longer resonant at the operating frequency. When an "electrically short" dipole is used, it's input impedance Zin = Rs + j · Xs appears capacitive and the series resistive component becomes smaller, approximately proportional to the square root of the physical length. This results in a "high Q feed impedance" requiring the reactive term to be tuned out with a corresponding inductive reactance. The energy losses associated with this resonating inductance can be significant, especially as the dipole dimensions are reduced. If the "Q" of the resonating inductor equals the "Q" of the dipole antenna then the antenna efficiency will equal one half as one half the (receive or transmit) energy will be lost in the inductor's resistive component and one half in the "radiation resistance" Ra of the antenna.
MATHCAD example
I found an equation that predicts radiation resistance Ra for an electrically short dipole antenna derived from Maxwell's equations. The expression can be presented as
Ra = 49.25 · γ 2 Ohms ...(14a)
where γ represents a "fractional length ratio" of the dipole's total length L compared to the theoretical half wave length λ/2 defined as γ ≡ L / ( λ/2 ) . This formula assumes that γ << 1
I then found some radiation resistance data for a vertical ¼ wave antenna placed over a "near infinite" conductive ground plane from a very old radio engineering handbook
The top row refers to the radio frequency wavelength compared to the length of the antenna set to be one quarter of a wavelength. The first entry "1" implies that ¼ of the radio signal wavelength equals the electrical length of this antenna and this ratio increases as lower frequency radio waves are tested. The bottom row contains the measured radiation resistance for this ¼ wave antenna used at or below its electrical length (yes, not a very intuitive approach for data presentation)
I used the reciprocal of the top row to show "fractional length" γ compared to a ¼ wave antenna as before. I also multiplied the radiation resistance of the single ¼ wave antenna by two to represent a ½ wave dipole that can be considered as two ¼ wave antennas in series.
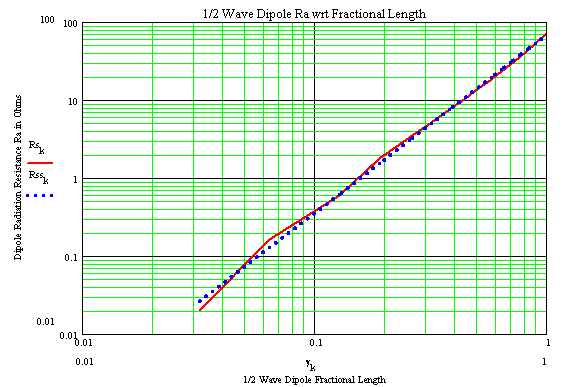
The log-log graph scale shows a linear relationship corresponding to a power relationship
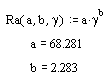...(14b)
We see the proposed equation (blue dotted line) shows good agreement with the red measured line. Some kinks are presumable the result of measurement error.
The slightly greater than square power fall off in radiation resistance is not unexpected as this "fudges" an approximation to a small correction term that would be needed to incorporate the loss of directional gain for electrically short dipoles (these tend towards becoming omni directional). This square law relationship can be understood as a "conversation of energy" requirement. Imagine that a ½ wave dipole antenna is reduced in length by one half. The resulting Hr magnetic field magnitude will also halve so the power density Sd will drop by one quarter from equation (9). Since energy cannot be created or destroyed (unless we have another "big bang") the input power to this electrically short antenna must also be one quarter. If the input AC current is the same, it follows that the radiation resistance must also be one quarter the original value since Pr = (Iac )2 · Ra
I hope this "arm waving" description will provide an intuitive understanding for the slight differences between equations (14a) and (14b).
It may appear then that electrically short dipoles should perform equally as well as an isotropic antenna and almost as well as a half wave dipole (in terms of antenna gain). However, practical limitations exist when trying to match a low radiation resistance to a more standard typical value of 50 Ohms used in many RF systems. For example, the previous VHF half wave antenna could be shrunk in length by a factor of 10 to 1 i.e. γ = 0.1. The previous graph shows a radiation resistance of only Ra = 0.4 Ohms. It is likely that significant power losses will occur in the matching network required to transform this low resistance up to 50 Ohms. Further, the electrically short antenna will exhibit a significant series reactive component, possibly in the order of several thousand ohms of reactance (capacitive). This would need to be tuned out with an equal and opposite reactance. The "Q" of this ratio is Q ~ 3000 / 0.4 = 7,500.
If the components used in the matching network had infinite Q then no power would be lost but the antenna bandwidth would be small (-3 dB at Δf = f / 7,500). However, such components do not readily exist and even if they did, they would most probably not suit a small portable application.
An even further problem is associated with "de-tuning". Even if this shortened antenna could be used, it would be extremely sensitive to nearby objects that could add small additional capacitive loading and shift the antenna's resonant frequency.
It can be seen that an electrically shortened dipole may be feasible but not necessarily practical. Even at one tenth dimension, this VHF example dipole antenna would still be 0.1 meters total length and not fit into a small matchbox sized pager!
The Magnetic B Field antenna was developed to address many of the issues confronting the electrically short dipole. It is required to be physically small compared to a wavelength, have adequate radiation efficiency, provide some means to present a "reasonable" terminal impedance and be relatively insensitive to detuning effects caused by nearby objects.
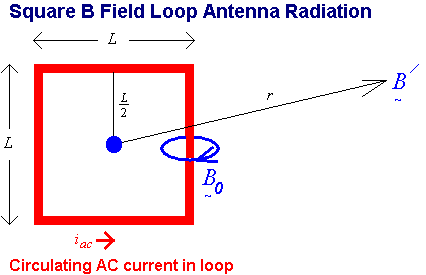
The simplest loop antenna consists of a wire loop with an AC Iac current flowing in the loop. This current generates a magnetic field that is responsible for radiation, in much the same way the previous dipole antenna operated. The inductance of this loop is predictable (as I described in my previous web chapter on inductors) and can be "tuned out" with a capacitor placed across a gap in the loop.
This style of antenna is often used for direction finding and has a sharp "reception null" when turned broadside to the incoming magnetic field. The "ferrite rod antenna" used in small AM broadcast radios operates much the same way and will exhibit a signal null when pointed end on to a radio station.
Magnetic loop antennas also receive great interest from radio amateurs for transmission and reception at frequencies below 30 MHz and where available space required for a full dipole antenna is unavailable. I have found many excellent implementations on the web that have achieved radiation efficiencies that are comparable to a standard dipole despite useful reductions in size.
Magnetic loop antennas have some interesting directional advantages. Sometimes it is advantageous to have a directional response but in some cases it may be convenient to communicate in any direction over the surface of the earth. A vertical dipole will achieve this and produce "vertically polarized" radiation that has equal power in all directions around it. However this may be cumbersome for long dipoles. For example, a ½ wave dipole required for operation in the 80 meter amateur band would need a tower that would be at least 40 meters high! A horizontal dipole is much easier to implement, but has a "blind spot" to signals arriving at its ends. A magnetic loop antenna solves this problem. It can be placed horizontally relative to the ground and produce horizontally polarized radiation in all horizontal directions. It is also claimed that "ground effects" are less problematic for magnetic loop antennas compared to dipoles.
Some accidental reception from the electrostatic component of the incoming wave may occur due to the physical area of the conductors used in the loop antenna. This reduces the depth of the reception null as some residual energy pick up remains.
This unwanted pick-up can be avoided by placing an electrostatic shield around the loop antenna.
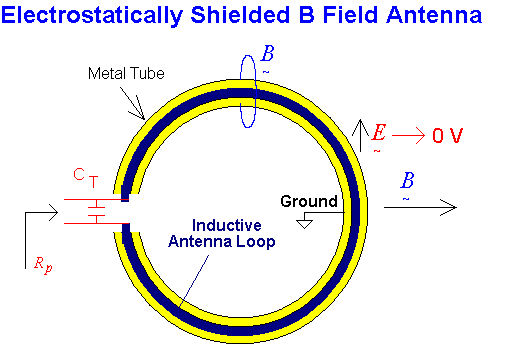
A metal tube can be used as shown. Note that a "gap" is needed to prevent the metal tube from acting like a shorted turn. The metal tube is grounded and the electrical connection is made to the magnetic loop either at its highest impedance point or over some fractional segment of its circumference. Although a balanced connection is preferred and offers greater rejection of stray electrostatic pick-up, and unbalanced connection is also feasible.
The circular loop is popular at low radio frequencies and may contain many turns of wire, resulting in a higher, more practical inductance. At higher VHF frequencies it may be desirable to "print" the antenna on a PCB as a square copper trace.
This configuration can be printed on an internal PCB layer and "sandwiched" between a top and bottom copper sheet acting as the previous metal tube for electrostatic shielding. In this case the "gap" can be implemented as a "slit" in the top and bottom copper shields in order to prevent these acting as a shorted turn and so interfering with the magnetic loop antenna's proper operation
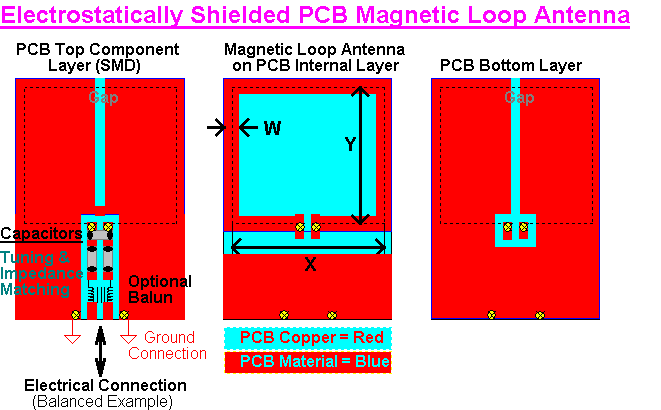
This PCB magnetic loop antenna uses an internal PCB copper track as the radiating element. Top and Bottom copper sheets provide electrostatic shielding (i.e. eliminating potential "hand capacitance" detuning effects from nearby conductive objects). An insulating "gap" is need in these shields to prevent the formation of a shorted turn as this would seriously interfere with the magnetic loop antenna's operation.
The inductance of the magnetic loop is "tuned out" with a parallel capacitor as shown (placed on the top PCB layer). Two series capacitors are then included to provide an impedance transformation, and the tuning capacitor's value is reduced to compensate for their additional capacitance. (PCB Via connections are shown a yellow circles with a cross)
An optional balun may be included, allowing either a balanced electrical connection (e.g. twisted wire or 300 Ohm ribbon cable) or an unbalanced connection (e.g. 50 Ohm coax). In both cases the copper shields must be connected to a suitable adjacent ground point (otherwise they will act like plate antennas and capacitively couple electrostatic signal energy into the loop antenna)
The loop matching can also be implemented along a segment of the loop. The length of this segment can be adjusted to achieve a direct impedance match (a single resonating capacitor is still needed)
Finally, multiple turns can be implemented to achieve higher inductance as may be required for lower frequency operation. These loops can be implemented as concentric track "square spirals" and multiple internal layers can be used to stack these PCB track spirals on top of each other with via connections.
The ferrite rod magnetic loop antenna is popular for AM radios and has also been used in some (usually older) Shortwave radios.
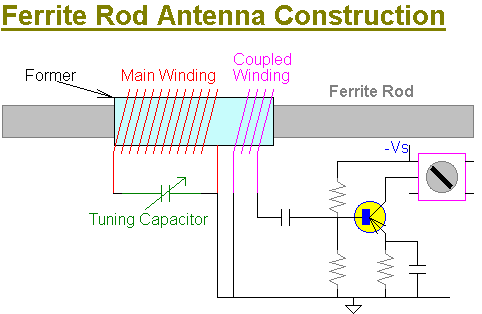
The ferrite composition is required to exhibit low losses at the intended operating frequency and medium relative permeability e.g. μr ≈ 50. The actual efficiency is extremely low (i.e. less than 0.1 % compared to a dipole) but this deficiency is more than compensated for by its convenient small size, essential for portable radios, and the characteristic high "atmospheric noise" associated with low radio frequencies (the actual noise floor can be 50 dB higher than thermal noise, so an antenna with -50 dB loss is not problematic!)
The overall efficiency of a magnetic loop antenna is defined as the amount of power transmitted as radio signal energy compared to the energy transmitted by a loss-less isotropic antenna. Since antennas are reciprocal, transmit efficiency and receive efficiency are exactly equal.
The magnetic loop antenna could be made diminishingly small and retain 100 % efficiency. However this performance requires that conductor power losses are zero in addition to any associated dielectric losses. Further, the operating bandwidth will diminish eventually to zero! Clearly some practical limitations need analysis
The ohmic conductor losses are common to all magnetic loop antennas, whether they have a circular, octagonal, hexagonal, square or triangular shape. The total loop resistance is proportional to the total length l and is affected by the conductor diameter (if circular) and the operating radio frequency (RF)
The most common conductor used for magnetic loop antennas is copper (or silver plated copper). Copper has a typical DC resistivity of
...(15)
The
DC resistance of a length l of wire
with radius r and resistivity ρ
becomes
…(16)
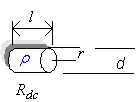
For
example, a 40 mm length of 1 mm diameter copper wire predicts that Rdc
= 852
μΩ
.
Unfortunately the actual conductor resistance increases with AC frequency and the DC value has little bearing on the actual value. This is caused by a "skin effect" phenomenon that tends to cause the AC current to travel close to the surface of a conductor as opposed to its central mass. This reduces the "effective" area or the conductor resulting in a higher AC resistance
We now have to consider the effective area of the (cylindrical) conductor based on its circumference multiplied by this effective "skin depth" δ.
In reality the current density J falls off exponentially as the radial distance r is reduced according to
...(17)
The skin depth coefficient δ is related to the DC resistivity and the operating frequency according to the following equation
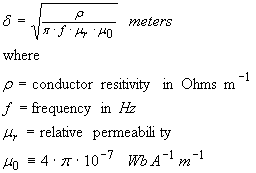...(18)
If we use non magnetic conductors such as copper, silver or aluminium the relative permeability μr = 1. Equation (18) now simplifies to
...(19)
For example, the skin depth δ for copper at f = 150 MHz will be only δ = 5.32 μm. This skin depth is extremely thin compared to the diameter d = 2 · r of most available wires (they may as well be hollow!).
The "effective area" Ae of this wire will be defined as Ae = 2 · π · r · δ in comparison to the actual area A = π · r 2 (Ae < A when δ < ½ · r). Substituting the skin depth equation (19) into this expression for effective wire area leads to
...(20)
where the wire diameter d is used instead of radius r i.e. d ≡ 2 ·r
The actual AC or RF resistance of this cylindrical wire can be predicted by substituting this effective area Ae into the DC expression for resistance in equation (16) resulting in a new AC resistance Rac
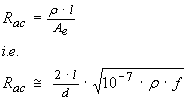...(21)
It may be helpful to represent this AC resistance Rac in terms of a "fractional wavelength" γ instead of the actual wire length l i.e. l ≡ γ · λ where λ ≡ c/f . Equation (21) can now be expressed in terms of this fractional wavelength γ
...(22)
where the resistivity of copper is ρ = 1.673 10-8 Ω m-1 and the fractional bandwidth γ will be assumed to be less than one i.e. γ << 1 for an electrically small antenna.
It may seem odd that the AC resistance now appears to reduce in an inverse square-root fashion with frequency f but this can be misleading as the use of this new fractional wavelength term γ implies a shrinking length of wire as this frequency increases. If the length of wire l remains constant, the AC resistance Rac is predicted from equation (21) and increases with the square root of frequency f . However, a constant fractional wavelength implies that the wire length would halve if the frequency doubles and this "over-rides" the inverse square root increase, hence equation (22)
Equation (22) can now be presented for copper conductors in its simplest form using the published resistivity ρ = 1.673 10-8 Ω m-1 for copper wire e.g.
...(23)
For the purpose of illustrating the difference between DC resistance Rdc and AC resistance Rac let's return to the previous d = 1 mm copper wire example with length l = 40 mm and consider a VHF frequency of f = 150 MHz i.e. λ = 2 meters. The DC and AC resistances become
Rdc = 852 μΩ
Rac = 40.07 m Ω
We see that the RF resistance Rac is 47 times higher than the DC resistance Rdc !
If we want to predict this ratio of RF to DC resistance for some other purpose, it can be expressed as
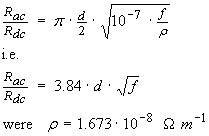...(24)
We can interpret equation (24) as demonstrating increased "skin effect" losses as frequency increases and also that very small diameter conducting wire will tend to not exhibit significant additional skin effect losses since the skin depth will be comparable to the actual wire radius. In both cases however, increased wire diameter will always reduce ohmic loss.
Note 1: The variable l refers to the total conductor length and is independent of the actual magnetic loop antenna shape
Note 2: A Printed Circuit Board (PCB) magnetic loop antenna will also be affected by "skin depth" effects. In this case, the "effective area" Ae will become Ae = 2 · w · δ were w represents the width of the copper trace and the factor of 2 accounts for current flow on the top and also the bottom of the PCB trace.
Note 3: The overall surface finish also affects the RF resistance. Rough surfaces will appear to be longer than a smooth surface as the current flow has to accommodate small peaks and hollows. This "surface roughness" may need to be included if optimal prediction accuracy is required.
Note 4: Although material parameters are often presented in non SI units e.g. micro-ohms per cm, these conventions change with the times so I will use standard SI units where possible for equations, e.g. resistivity is in Ohms per meter. However it may be convenient to use units of MHz for frequency f in equation (23) as this will return a value of AC resistance for Rac in milli-ohms m Ω
We can predict the radiation resistance Ra for a magnetic loop antenna by first considering its open circuit voltage E when a time variable magnetic flux Ø passes through its enclosed area A.
We know from physics that the magnetic flux Ø equals the product of a magnetic field B and the loop area A so that
Ø = B · A ...(25)
Since B = μ · H were μ ≡ 4 · π · 10-7 we also have
Ø = μ · H · A ...(26)
The open circuit voltage (EMF) induced in the loop is proportional to its area and the rate of change of magnetic flux i.e.
EMF = -∂Ø / ∂t = -μ · A · ∂H / ∂ t ...(27)
Let us now consider an sinusoidal oscillating magnetic field with a peak value Hp and frequency f.
H ≡ Hp · sin{ 2 · π · f · t } ...(28)
Substituting equation (28) into equation (27) now reveals that
EMF = -∂Ø / ∂t = -2 · π · f · μ · Hp · A · cos{ 2 · π · f · t } ...(29)
The RMS magnitude E of this induced voltage will be
E = √2 · π · f · μ · Hp = 2 · π · f · μ · Hrms · A ...(30)
were Hrms represents the RMS magnitude of the magnetic field H.
In order for power to be extracted from this magnetic loop antenna, we require this EMF, or some proportion of it to the presented to a load resistance. We know that optimum power transfer occurs when the load resistance equals the source resistance and any reactive components are cancelled. The electrically short magnetic loop antenna will have a series inductive reactance and we will imagine that this component is first cancelled with and equal value of capacitive reactance. The magnetic loop antenna will then appear as a voltage source in series with its radiation resistance Ra. To achieve maximum power transfer the load resistance will also equal Ra and the AC voltage appearing across it will equal ½ · E.
This might seem odd - one half the received power is dissipated in the load resistance and one half in the antenna's radiation resistance. Were did this "other half" power go?
Presumably it gets radiated back into space!
Since P = v2 / R it follows that the received power Pr will be
Pr = ( π · f · μ · Hrms · A)2 / Ra ...(31)
We now need to relate this RMS magnetic field magnitude Hrms to transmitted power and perhaps compare the power Pr received by this magnetic loop antenna to other antenna varieties. We know that the magnetic field Hrms is related to power density according to
Sd = 377 · (Hrms )2 were Sd = Pin / [ 4 · π · d 2 ] i.e. (Hrms )2 = Pin / [ 4 · π · 377 · d 2 ]
Substituting this result into equation (31) then predicts
Pr = Pin · π · f 2 · μ2 · A2 / [Ra · 4 · Rεμ · d 2 ] ...(32)
where Rεμ is called the "impedance of free space" with an approximate value of Rεμ = 377 Ohms.
Magnetic loop antennas have a directional response that is similar to that of a dipole. Therefore it makes sense to compare the received energy from a magnetic loop antenna with the energy received by a half wave dipole.
Recalling equation (12 ) we predicted that the power Pr received by a half wave dipole from a isotropic radiating source with an input power Pin was
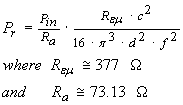...(12)
Since antennas are reciprocal, the same power Pr will be retrieved when a half wave receiving dipole is used with an isotropic transmitting antenna. I consider the case of an isotropic transmit antenna combined with a dipole receiving antenna to be "equivalent" to the same isotropic antenna combined with a magnetic loop antenna. In the absence of any ohmic losses, both must be capable of receiving the same electromagnetic power energy.
In other words the receive power Pr in equation (32) must equal the received power Pr in equation (12)
OK, so let's set Pr in equation (12) equal to Pr in equation (32) and make the magnetic loop antenna's radiation resistance Ra the subject (and denote the dipole antenna's radiation resistance as R /a in order to prevent confusion). The result after some algebra is
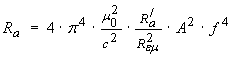...(33)
Equation (33) now demonstrates the extreme sensitivity for the magnetic loop antenna's radiation resistance Ra with loop area and especially with frequency. Let us consider an example square loop antenna with the same dimensions I used previously for AC resistance Rac predictions, i.e. l = 40 mm total wire length with f = 150 MHz ( λ = 2 meters). The implies that the loop area A = 1 · 10-4 m2 .Using R/a = 73.13 Ohms and Rεμ = 377 Ohms we predict that
Ra = 3.518 · 10-30 · A2 · f 4 = 17.81 μΩ !
Now recall the AC resistance of this length of wire was Rac = 40.07 m Ω - obviously this VHF magnetic loop antenna design will have extremely low efficiency! The actual efficiency will be determined by the ratio of these two series resistances, e.g.
η ≡ 100 · Ra / ( Ra + Rac ) % ...(34)
From this example we predict that η = 0.0442 %
I hope the discussion so far has provided an intuitive understanding for magnetic loop antennas based on relatively straight-forward Physics without the distractions of Maxwell's equations. This intuitive approach is useful as it let's us make some reasonable predictions on how to make electrically small magnetic loop antennas with some constraints governed by efficiency relative to a half wave dipole. So far we have learnt that
 | The AC resistance Rac of a conductor increases with frequency due to "skin effect" in a predictable way and dominates the DC resistance Rdc |
| This AC resistance is proportional to the length of wire conductor l and inversely proportional to wire diameter |
| The AC resistance does not depend on the loop geometry (shape) |
| This AC resistance Rac is in series with the antenna's "radiation resistance" Ra and results in a loss of power that can be represented as a comparative efficiency relative to a half wave dipole |
| The efficiency of an antenna is determined by the ratio of radiation resistance to "AC (loss) resistance plus radiation resistance" |
| The radiation resistance increases with loop area so geometries that maximize area for a given conductor length will provide the highest radiation resistance and consequently the highest efficiency |
Well this reasoning is certainly easier to conceptualize than trying to muddle through a haze of differential and integral equations combined with boundary conditions! We can readily guess that a circular loop will provide the highest area for a given length of conductive wire and consequently exhibit optimum efficiency for any given frequency. An octagonal geometry will provide slightly less area and therefore reduced efficiency, followed by a hexagonal geometry, then a square geometry and finally a triangular geometry (a "folded dipole" requires a different analysis as its area approaches zero but has a radiation impedance close to 300 Ohms).
Some examples of Area Ax to total conductor length l are
Acircle = l 2 / ( 4 · π ) ≈ I 2 / 12.57
Asquare = I 2 / 16
Atriangle = I 2 / (12 · √3 ) ≈ I 2 / 20.78 (assuming equal sides)
It may be useful to express equations (33) and (34) in terms of fractional wavelength defined as γ ≡ l / λ
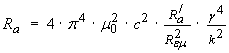... (35)
where k = 12.57, 16 or 20.78 for circle, square or
triangle geometries.
Combining these constants then produces a simple result
...(36)
Once again. using l = 40 mm at f = 150 MHz results in γ = 0.02 and the following predicted radiation resistances
Ra = 28.85 μΩ for a circular loop geometry were k = 12.57 so that efficiency η = 0.0719 %
Ra = 17.81 μΩ for a square loop geometry were k = 16 so that efficiency η = 0.0442 %
Ra = 10.56 μΩ for a triangular loop geometry were k = 20.78 so that efficiency η = 0.0263 %
Since the magnetic loop conductor loop was constant across all three examples, the AC resistance has the same value of Rac = 40.07 m Ω. We observe the circular loop to exhibit the best efficiency, followed by the square magnetic loop, slightly better than one half the efficiency of the circular loop. The triangular loop is, not surprisingly, even worse again !
It should be remembered that high antenna efficiency and small antenna size are mutually exclusive. The magnetic loop antenna efficiency can be improved by using wire with a higher diameter as suggested from equation (23)
...(23)
If large antennas are required, copper tubing can be used to advantage, or copper sheet or even printed circuit boards soldered together as panels in a pseudo-circle!
Let us consider a HF example at f = 30 MHz (λ = 10 meter band). Let's consider using l = 2 meters of hollow copper tubing for the magnetic loop antenna with a diameter of d = 10 mm. This length to wavelength ratio implies that γ = 0.2.
Since right angle bends are difficult we will use a circular geometry i.e. k = 12.57. The AC resistance, radiation resistance and efficiency will be
Rac = 0.0896 Ohms
Ra = 0.289 Ohms
η = 76.3 %
This represents a power loss of only 1.17 dB compared to a dipole. Given that the magnetic loop diameter will be only 2 / π = 0.637 meters compared to a half wave dipole that requires a corresponding length of 5 meters, this small 1.17 dB power loss could be a small price to pay if space is at a premium.
So it appears that the magnetic loop antenna can be designed with excellent results providing that realistic dimensions are chosen. However it does have an Achilles' heal. I mentioned before that the series inductance of the loop will need to be "tuned out" with an equivalent capacitive reactance, forming a tuned circuit topology. This will probably have a very high Q due to the small resistive terms involved. As a direct consequence, the magnetic loop antenna will have a narrow operating bandwidth and may need retuning even for small frequency changes (e.g. with an amateur radio band)
I have seen many impressive approaches to this on the Internet were a number of radio amateur enthusiasts have combined geared motors to the shafts of air dielectric variable capacitors and operated these remotely.
We have actually done all the "hard theoretical work" by now so this web section should be easy. We first recall the expressions for AC resistance and radiation resistance
...(23)
...(36)
where fractional wavelength defined as γ ≡ l / λ and the scaling term k is geometry dependent i.e. k = 12.57, 16 or 20.78 for circle, square or triangle geometries. The total resistance is equal to the sum of Rac and Ra
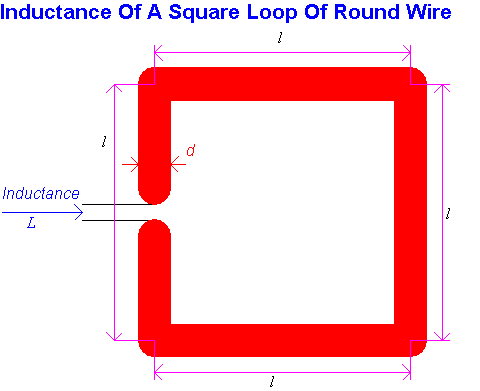
This combined resistance is also in series with the loop inductance that I presented in the previous web chapter on Inductors as
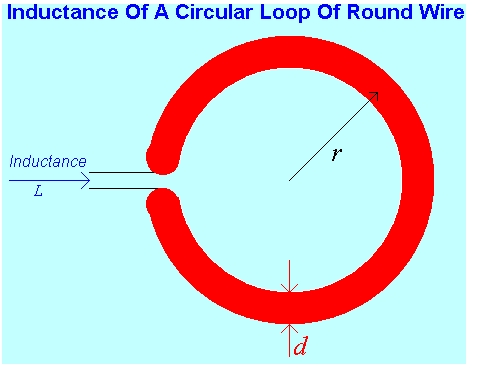
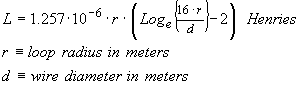...(37)
Providing r > 2.5 · d
The inductive reactance Xs of this loop is Xs = 2 · π · f · L
The capacitance Cs required to tune this reactance out is Cs = 1 / [ 2 · π · f · L ]
The "Q" of the loop will be Q = ½ · Xs / [ Rac + Ra ]
Note: The total loop resistance is in series with the equal value of load resistance (matched for optimum power transfer) so the expression for operating Q contains the ½ scale term.
The -3 dB bandwidth of the loop will be BW-3dB = f / Q. The actual operating bandwidth may be considerably lower especially if low VSWR performance is required for transmission.
Let us return to the previous example for f = 30 MHz with l = 2 meters of hollow d = 10 mm copper pipe used for the magnetic loop antenna. The fractional wavelength γ of this total length is γ = 0.2 (larger values of γ may result in less accurate predictions as the currents and voltages within the loop may start to have significant time delays and corresponding phase shift errors)
Predictive Results
f = 30 MHz (10 meter amateur radio band)
l = 2 meters (total length of copper tubing)
d = 10 mm (average diameter of copper pipe)
γ = 0.2 (fractional wavelength)
Rac = 0.0896 Ohms (Loop AC resistance at f = 30 MHz)
Ra = 0.289 Ohms (Loop radiation resistance at f = 30 MHz, k = 12.57 for a circular loop)
Rtotal = 0.379 Ohms (Total loop resistance at f = 30 MHz)
η = 76.3 % (Best case efficiency for resonant loop antenna with no additional power losses)
r = ½ · l / π = 0.318 meters (Radius of magnetic loop antenna)
L = 1.69 μH
Xs = 318.6 Ohms
Q = 420.3
BW-3dB = 71.4 kHz
We can see that very high Q components will be required for tuning (and impedance matching to 50 Ohms) in order to prevent additional losses. Also the -3dB bandwidth is extremely low and retuning will be needed for even minor changes in frequency
The magnetic loop geometry affects the loop's radiation resistance and its inductance. The AC loss resistance is not affected however.
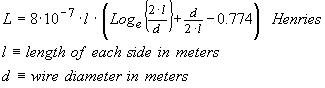...(38)
Predictive Results
f = 30 MHz (10 meter amateur radio band)
l = 2 meters (total length of copper tubing)
d = 10 mm (average diameter of copper pipe)
γ = 0.2 (fractional wavelength)
Rac = 0.0896 Ohms (Loop AC resistance at f = 30 MHz)
Ra = 0.178 Ohms (Loop radiation resistance at f = 30 MHz, k = 16 for a square loop)
Rtotal = 0.268 Ohms (Total loop resistance at f = 30 MHz)
η = 66.5 % (Best case efficiency for resonant loop antenna with no additional power losses)
l = ¼ · l = 0.5 meters (length of each side of the square magnetic loop antenna)
L = 1.54 μH
Xs = 289.6 Ohms
Q = 540.3
BW-3dB = 55.5 kHz
The square magnetic loop antenna exhibits slightly lower efficiency than the circular magnetic loop antenna constructed from the same length of copper tubing (η = 66.5 % compared to η = 76.3 % ) and slightly lower bandwidth (BW-3dB = 55.5 kHz compared to BW-3dB = 71.4 kHz)
Does this mean that a circular loop antenna is always better? Well maybe not. Let's imagine a confined space that has a maximum square dimension as might be available on a balcony. The previous circular loop antenna example would have a diameter equal to 0.6366 meters for 2 meters of copper tubing. Let's consider what would happen if a square magnetic loop antenna could also fit this area and have sides equal to 0.6366 meters i.e. its total conductor length l could now become l = 2.546 m. This time we would have
f = 30 MHz (10 meter amateur radio band)
l = 2.546 meters (total length of copper tubing)
d = 10 mm (average diameter of copper pipe)
γ = 0.2546 (fractional wavelength)
Rac = 0.1141 Ohms (Loop AC resistance at f = 30 MHz)
Ra = 0.468 Ohms (Loop radiation resistance at f = 30 MHz, k = 16 for a square loop)
Rtotal = 0.582 Ohms (Total loop resistance at f = 30 MHz)
η = 80.4 % (Best case efficiency for resonant loop antenna with no additional power losses)
l = ¼ · l = 0.6365 meters (length of each side of the square magnetic loop antenna)
L = 2.08 μH
Xs = 392.4 Ohms
Q = 337.1
BW-3dB = 89.0 kHz
Well well well. Now the square magnetic loop is "better" than the circular magnetic loop antenna if the surrounding space is applied as a constraint. It just goes to show that it is best to not jump to a conclusion prematurely!
As we have seen the magnetic loop antenna presents a rather inhospitable and daunting impedance to the relatively benign 50 Ohm resistive outside world. We therefore need to devise suitable strategies to tame the loop impedance in order for it to coexist with standard communication equipment and impedance interfaces that are typically defined at a resistive value of 50 Ohms.
There are (at least) three general strategies for impedance matching
| Capacitive Impedance Transformation |
| Inductive Tap Impedance Matching |
| Coupled Inductive Loop Impedance Matching |
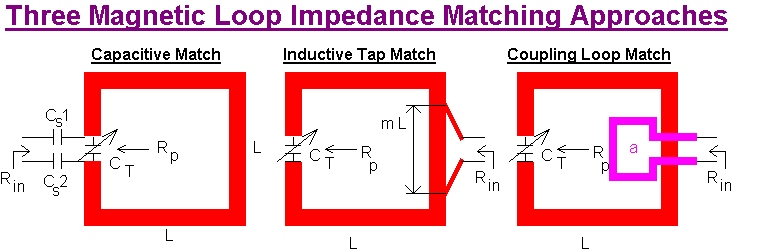
The capacitive impedance matching approach relies on series to parallel impedance conversion that can be presented as
Rp = Rs ( 1 + QT 2 ) ...(A)
Xp = Xs (1 + QT -2 ) ...(B)
QT ≡ Xs / Rs ≡ Rp / Xp ...(C)
The variable QT represents a "transformation Q" and is not directly related to actual operating Q although both will show similar trends. Let us consider the last square magnetic loop example.
Rs = 0.582 Ohms and Xs = 392.4 Ohms → QT = 674 → Rp = 264567 Ohms, Xp = 394.4 Ohms
We need to transform the loop impedance in parallel form to 50 Ohms
From equation (A) with Rs = 50, Rp = 264567 we find that QT = 72.73 (note that QT is just a parameter for this procedure)
QT = 72.73 → Xs = 3636.5 (equation C) → Cs = 1.459 pF at f = 30 MHz → Cs1 = Cs2 = 2.918 pF (i.e. in series)
Also Xp = 394.4 Ohms → CT = 13.45 pF at f = 30 MHz
This CT represents the total parallel tuning capacitance presented to the loop and part of this is provided by the series capacitors Cs1 and Cs2. From equation C we have Xp = Rp / QT = 3637.7 Ohms → Cp = 1.458 pF at f = 30 MHz
We need to subtract this additional Cp from CT i.e. the corrected value of CT = 11.99 pF
We have determined that a tuning capacitor will be needed with a nominal value of 12 pF for this magnetic loop antenna and two coupling capacitors each equal to 2.9 pF will be need to transform the loop impedance down to a balanced value of 50 Ohms. A balun may be included to convert balanced to unbalanced.
The capacitive impedance match is easy to implement except that all three capacitors need to have high voltage ratings. Since we know the effective parallel resistance of the loop, i.e. Rp = 264567 Ohms, we could reason that a segment of the loop conductor would act like an "auto transformer" compared to its open end. For example, a segment equal to 1/10th the total conductor length will have 1/10th the voltage impressed over it compared to the open end and so therefore have an effective parallel resistive component equal to Rp / 100. In general, if we define the segment length to be m · L where L = the length of one side and 4 · L = the total loop length then we should have
m = 4 · L ·√ (50 / Rp ) = 0.01375
Since each side had length L = 0.6366 meters we have a segment length m · L = 35.01 mm
The tuning Capacitor will be relatively unaffected (no additional reactive load added) so CT = 13.45 pF
This method can also be used to provide an unbalanced impedance match simply by shifting the ground connection to the loop center - this also allows the tuning capacitor body (ground) to be connected to the same ground point as both will be at the same RF voltage = 0 V.
Butterfly tuning capacitors are best - the main RF current does not need to pass through potentially high loss contacts.
Although this central connection is at "ground" no balance is perfect. Do not touch the ground if you are supplying even small amounts of RF power to the loop antenna as you may get a nasty RF burn.
If you try full power you may not return from your experimentation.
This is probably best tried by experiment. The coupling loop may benefit from an additional tuning capacitor and could be moved relative to the mail magnetic loop to optimize the final impedance match.
The actual impedance ratio will probably be related to a ratio of the two areas.
I hope my web chapter on magnetic loop antennas has been interesting and useful in this Component Universe. These antennas can be purchased already made but can equally be designed and built by amateur radio enthusiasts. The offer a controlled tradeoff between size, efficiency and operating bandwidth and suit applications where space is at a premium
In this web chapter we started with an analysis of the half wave dipole antenna. This served as reference for other antenna formats. We explored the path loss equation for an isotropic to isotropic antenna (i.e. theoretically omni-directional) and defined the "aperture area" for such an antenna.
We then compared the path loss for a isotropic transmitting antenna to a receiving dipole antenna and found a gain of about 2.15 dB, attributable to its directivity.
The concept of "radiation resistance" was also presented, along with the concept of "skin depth" in a conductor with its associated increase in power loss at higher AC / RF frequencies. This, in comparison with an antenna's radiation resistance determines its efficiency. The radiation resistance of a half wave dipole was defined at 73.13 Ohms (to 4 significant figures)
The concept of reciprocity was invoked to use the isotropic antenna as a transmitting source and the dipole as a receiving directional detector. The path loss is unchanged by this swap-around. Since the magnetic loop antenna has similar directivity to a dipole, it was used in comparison to determine the radiation resistance of the magnetic loop antenna.
Some associated concepts were included in this somewhat meandering derivational path. For example, the energy density S over the surface of a sphere was related to magnetic field magnitude H at a distance. The "impedance of free space" = 377 Ohms was also included in these conversions.
A number of magnetic loop topologies were proposed, e.g. circular, octagonal, hexagonal, square and triangular. The directivity improvement resulting from electrostatic shielding was indicated, and a hollow tube method and a PCB method was shown.
Equations were presented for antenna efficiency, impedance and tuning capacitance. Operating Q and bandwidth estimates were also provided.
Some useful generalizations "fell out" in this process I guess
| The AC resistance of a loop antenna depends on the total length of the conductor, its diameter and the DC resistivity of the material and also the actual RF frequency |
| The radiation resistance increases with loop area to a forth power and is highest for a circular geometry if the total length is constant. This need not represent a real world constraint as a square loop gave better results in one example I presented! |
| Antenna efficiency is best if the radiation resistance is much grater than AC conductor loss resistance (no surprise there!) |
| The magnetic loop antenna will exhibit series inductance. The circular loop will exhibit the highest inductance |
| The magnetic loop antenna will tend to have an extremely high operating Q and therefore a narrow frequency bandwidth |
Consistent with the phrase "you can't get something for nothing" is another "you cant get 100 % antenna efficiency with minimal space and high operating bandwidth". It seems that engineering a magnetic loop antenna is, once again, the art of compromise.
Some real world examples were included to allow the reader to check the equations before attempting their own magnetic loop antenna construction projects! Also I have shown three methods that could be used to match the loop impedance to a standard 50 ohm resistive value
Phew! I have to admit this web chapter took longer than I first thought. I hope the content will be of interest and helpful. I spent some time looking on the Internet for material as a reference to my derivations but there appears to be a number of competing formulas out there. Some of them have obvious errors, as do some programs (e.g. one program assumed that inductance didn't depend on the loop geometry)
In any case I hope my web chapter on magnetic loop antennas has provided a conceptual or near intuitive appreciation of the factors that determine the performance and design constraints and trade-offs that apply to them. I have avoided abstract Maxwell's equations in favor of simpler "first year university Physics" material for magnetic fields, flux, inductance, resistance etc.
What would really be fun? Have you got any old super-conductors in your junk box? If so, these would be great for making a zero loss magnetic loop antenna. If they really have zero resistance then it should be possible to make an 80 meter magnetic loop antenna fit through the eye of a needle.
However there may be a catch - the operating Q would need to be extreme and the bandwidth would tend to zero Hz as the magnetic loop antenna's size shrank to zero loop area as well!
It might pay to consider choosing your transmitting words sparingly and speak clearly and very slowly in your deepest possible voice.
Return to: A Component Universe
or: Ian Scotts Technology Pages
© Ian R Scott 2007 - 2008
